myjulykatsukito - Clasificación de los números

Existe toda una teorìa de los nùmeros, que clasifica a los números en:

Nùmeros Naturales: Es cualquiera de los números que se usan para contar los elementos de un conjunto. Reciben ese nombre porque fueron los primeros que utilizó el ser humano para contar objetos.

Estos asu vez se clasifican en:

Nùmeros Compuestos: Todo número natural no primo, a excepción del 1, se denomina compuesto, es decir, tiene uno o más divisores distintos a 1 y a sí mismo. También se utiliza el termino divisible para referirse estos números. Los 20 primeros números compuestos son: 4, 6, 8, 9, 10, 12, 14, 15, 16, 18, 20, 21, 22, 24, 25, 26, 27, 28, 30 y 32.
Nùmeros Perfectos: Es un número natural que es igual a la suma de sus divisores propios positivos, sin incluirse él mismo. Dicho de otra forma, un número perfecto es aquel que es amigo de sí mismo. Así, 6 es un número perfecto, porque sus divisores propios son 1, 2 y 3; y 6 = 1 + 2 + 3. Los siguientes números perfectos son 28, 496 y 8128.

2. Números Enteros: Los números enteros $mathbb{Z}$ son una generalización del conjunto de números naturales $mathbb{N}$ que incluye números enteros negativos (resultados de restar a un número natural otro mayor), además del cero. El hecho de que un número sea entero, significa que no tiene parte decimal. Los números enteros negativos pueden aplicarse en diversos contextos, como la representación de profundidades bajo el nivel del mar, temperaturas bajo cero, o deudas, entre otros. Los números enteros están formados por los enteros positivos, los enteros negativos y el cero. El 0 no se considera ni positivo ni negativo.

Estos a su vez se calsifican en:

Nùmeros Pares: Un número par es un número entero múltiplo de 2, es decir, un número entero $m$ es número par si y solo si existe otro número entero $n$ tal que:

$m = 2 cdot n$

Por lo tanto, si multiplicamos cualquier número entero por un número par obtendremos un nuevo número par. Los siguientes son números pares: 0, 2, 4, 6, ..., y también: -2, -4, -6 ... .

Nùmeros Impares: Los números impares son aquellos números enteros que no son pares y por tanto no son múltiplos de 2. Los siguientes son números impares: 1, 3, 5, 7, 9 ..., y también: -1, -3, -5, ... . Sumando o restando 2 a un número impar se obtiene otro número impar. Sumando o restando una unidad a un número impar se obtiene otro número par. Se dice que un número entero, $m$ , es impar si y solo si existe otro número entero, $n$ , tal que: Nº= X+1

3. Nùmeros Racionales: En sentido amplio, se llama número racional a todo número que puede representarse como el cociente de dos enteros con denominador distinto de cero (una fracción común). El término «racional» alude a «ración» o «parte de un todo», y no al pensamiento o actitud racional.

4. Nùmeros Reales: En matemáticas, los números reales son aquellos que poseen una expresión decimal e incluyen tanto a los números racionales (como: 31, 37/22, 25,4) como a los números irracionales, que no se pueden expresar de manera fraccionaria y tienen infinitas cifras decimales no periódicas, tales como: 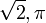$sqrt{2}, pi$ .

Estos se clasifican en :

Numeros Irracionales: En matemáticas, un número irracional es cualquier número real que no es racional, es decir, es un número que no puede ser expresado como una fracción $frac{m}{n}$ , donde $m$ y $n$ son enteros, con $n$ diferente de cero y donde esta fracción es irreducible.
Nùmeros Algebraicos: Un número algebraico es cualquier número real o complejo que es solución de una ecuación polinómica de la forma:
$a_nx^n+a_{n-1}x^{n-1}+dots +a_1x+a_0 = 0,$
Donde:

$n > 0 (a_n ne 0)$ , es el grado del polinomio.

$a_i in mathbb{Z}$ , los coeficientes del polinomio son números enteros.

Nùmeros Trancendentes: Un número trascendente (o trascendental) es un tipo de número irracional que no es raíz de ningún polinomio (no nulo) con coeficientes enteros (o racionales). En este sentido, número trascendente es antónimo de número algebraico. La definición no proviene de una simple relación algebraica, sino que se define como una propiedad fundamental de las matemáticas. En general, si tenemos dos cuerpos $(K,+,cdot)$ y $(L,+,cdot)$ de forma que el segundo es extensión del primero, diremos que $alpha in L$ es trascendente sobre $K$ si no existe ningún polinomio $p in K[x]$ del que $α$ es raíz ( $p (α) = 0$ ).

5. Nùmeros Hiperreales: son una extensión del conjunto de los números reales que permiten entre otros formalizar algunas operaciones con infinitésimos, y probar algunos resultados clásicos del análisis real de manera más sencilla.

6. Nùmeros Complejos: El término número complejo describe la suma de un número real y un número imaginario (que es un múltiplo real de la unidad imaginaria, que se indica con la letra i).

7. Cuaterniones: Los cuaterniones (también llamados cuaternios) son una extensión de los números reales, similar a la de los números complejos. Mientras que los números complejos son una extensión de los reales por la adición de la unidad imaginaria i, tal que

i 2 = - 1

, los cuaterniones son una extensión generada de manera análoga añadiendo las unidades imaginarias: i, j y k a los números reales y tal que

i 2 = j 2 = k 2 = i j k = - 1

. Esto se puede resumir en esta tabla de multiplicación: la Tabla de Cayley (inglés).

	1	i	j	k
1	1	i	j	k
i	i	-1	k	-j
j	j	-k	-1	i
k	k	j	-i	-1

1, i, j, k, son entonces las "bases" de las componentes de un cuaternión.

8. Nùmeros Infinitos: El concepto de infinito aparece en varias ramas de la filosofía, la matemática y la astronomía. En geometría, el punto al infinito en geometría proyectiva y el punto de fuga en geometría descriptiva; en análisis matemático, los límites infinitos, o límites al infinito; y en matemática dentro de las teorías de números y de conjuntos. En todos los casos denota que el ente en cuestión no es finito en algún aspecto.

9. Nùmeros Transfinitos: Un número transfinito es un número cardinal o un número ordinal mayor que cualquier número natural. El término "número transfinito" fue introducido por el matemático alemán Georg Cantor.

10. Nùmero Negativos: Un número negativo es cualquier número cuyo valor es menor que cero y, lógicamente, que los demás números naturales: 1, 2, 3, etc. Se utilizan para representar pérdidas, deudas, disminuciones o decrecimientos, entre otras cosas.